Золотое сечение и пропорции

И.Ю.Г

«Видящий, да услышит –

Слышащий, да увидит…»

Явился ангел в круге мироздания,

Перстом нарисовал овал земли,

Крылами вывел карту мироздания,

И треугольник в вечности любви.

 

Эта статья – плод моих размышлений о соразмерности, соотношениях или, говоря в общем, о пропорциях. Эта важная тема, которая волнует всех, кто творит и хочет разобраться в законах красоты и мироздания. Надо сказать, что когда я учился, а это было в 70-х -80-х годах 1900 годов, оказалось, что информации на эту тему катастрофически не хватало. Мы по крупицам собирали эти знания и, нам казалось, что найдя какие-то факты и знания, мы открываем мир. Мы были окрыленными. Но как только начинали рисовать или лепить, оказывалось, что ты много не знаешь и не понимаешь, как буд-то идешь интуитивно в темноте не зная дороги. С годами приходило чувство осознания ремесла и чувства красоты, что-то ты открывал сам, а другое само находило тебя. Интуиция и опыт, чувство «прекрасного» помогало творить, но только тем, кто обладал талантом и стремлением работать в поисках совершенного. Откровения приходили во время сна или во время работы после некоторого времени бесплотных поисков. Однако вера не покидала меня, что однажды придет сновидение, и ты поймешь, КАК ВСЁ УСТРОЕНО. Конечно, это была иллюзия или утопия, кому как больше нравится. Однако накопленные знания и опыт, собственные открытия, а были и такие, привели меня к мысли, что необходимо все это собрать, обобщить, и подарить как откровения от Игоря  молодому поколению, дабы облегчить им путь к постижению твердыни творчества и созидания.

Представленные в этой статье знания обобщают многие стороны, которые охватывают ПРОПОРЦИИ – а это архитектура и скульптура, живопись и графика, дизайн и декораторство, прикладное искусство и керамика, мебель и металлоконструкции, театр и балет, фотография и многое другое, где важен талант художника, созидателя и творца. Касается это и всего, что нас окружает, так мир живет и развивается по законам природы или Божественных сил, к пониманию которых мы очень далеки. Законы мироздания действуют вне, а часто и вопреки желанию человека, и понять их, почувствовать их природу, уловить вектор развития, поможет людям абсолютно во всех начинаниях, с которыми они будут сталкиваться на протяжении их жизни, да и всего развития человечества.

Некоторые молодые и наглые математики и физики говорят: дайте нам законы и мы все создадим, как говорил Исаак Ньютон: «дайте мне точку опоры, и я переверну мир». Однако с опытом, понимаешь, что в реальной жизни (а не в искусственном опыте), всегда действуют несколько сил и неизвестных, которые кардинально могут изменить результаты экспериментов. В природе все настолько сложно и взаимосвязано, что если что-то исчезло (например, сгорело) здесь, то в другом месте (измерении) прибыло. Ничто в нашем мире не исчезает бесследно. Человеческое слово – это колоссальная сила, которая может изменить мир. В Библии сказано, что в «начале была тьма. И отделил Бог небо от тверди…И сказал Бог: «Да будет свет. И стал свет… ». Бог творил и созидал шесть дней, а на седьмой день, решил отдохнуть (осмыслить, что было сделано). Конечно, все это иносказательно, и возможно, а это уже доказано физиками и астрономами, создавалось миллионами лет. Однако пространство было другое и время текло по-другому. И оценить нам сейчас это очень сложно.

Как в молекуле или атоме действуют определенные силы, так и в человеке, как в микрокосмосе, (ведь Бог создавал человека по образу и подобию своему), мы открываем законы мироздания, которые действуют во Вселенной. Природа, как часть мироздания, соразмерна, гармонична и пропорциональна, в ней все взаимосвязано, и ни что не может быть отдельно от другого.

Еще греки говорили, «…по-видимому, необходимо разделять ”Законы Гармонии Природы” и “Законы Красоты Искусства”. “Законы Гармонии Природы” объективны и отражают стремление природных структур к “оптимизации”, “целесообразности”, экономии вещества и энергии. Как показывают современные исследования, законы гармонии природы тесно связаны с Золотым Сечением и числами Фибоначчи, причем связь эта обнаруживается на квантово-механическом и генетическом уровнях. Что касается “Законов красоты”, то эти “законы” субъективны, так как выражают вкусовые и религиозные предпочтения определенных групп людей. И вряд ли в этом направлении можно построить какую-то стройную теорию».

Недаром, физики любят повторять вслед Альбертом Эйнштейном, что «если формула красива, то она верна».

В этой статье я постарался проследить, как формировался поиск золотых пропорций в истории, как создавались каноны и формулы вычислений, как они влияют на наше мировосприятие, как они взаимодействуют с окружающим нас миром.

После зрелых размышлений, я понял, что как бы мы не доверяли арифметике, каждому творцу следует прежде всего сверять свое творение с биением своего сердца, так как мы сами, не сознавая того, и есть суть проявления тех законов мироздания по которым творил Бог, и следуя природе, вникая в её законы мы постигаем сами себя.

Введение- все о пропорциях

На протяжении тысячелетий люди стремились обустроить мир вокруг себя, построить себе жилище, сделать себе одежду, стать более развитыми. Любопытство и интерес к окружающему миру, его устройству одолевали людьми и, со временем, меняли его к лучшему.

Изучая природу вокруг себя, животных и птиц, землю и небо люди стали лучше понимать красоту мира. Захватывающие пейзажи заката и рассвета, горные долины и реки, вызывали у людей чувство чего-то возвышенного и прекрасного. И человек, живя в сообществе себе подобных, пытался создавать вокруг себя то, что ему помогало в жизни, что эстетически его влекло и вдохновляло.

Сначала это были вещи необходимые, полезные в быту, или то, что было связано с его занятиями: такими, как охота, рыболовство, обряды, свадьбы и другие необходимые действия.

Однако, с течением продолжительного времени, лучшие из людей поняли, что в основе прекрасного, в основе построения мира лежат законы, которые необходимо найти и применять. Тогда, используя эти законы, можно создавать города, строить красивые дома, делать красивую одежду, Комплекс специальных упражнений помогал создавать прекрасное тело.

Наблюдая за впечатляющими закатами и волнующими восходами, за пустынями, где барханы перетекающего как волны песка уходят ползучими дорожками к горизонту, там, где бескрайние степи уходят и упираются в чарующие по красоте и монументальности горы, где морская гладь, отражая близ лежащие утесы, уносится вдаль и сливается свои отражением с опрокинутым небом, там везде человек видел и чувствовал, что он соприкасается с чем-то великим и трудно объяснимым, с тем, что создано по божественным законам гармонии и порядка.

Наконец, изучая законы мироздания, миропостроения люди поняли, что в основе «прекрасного» лежат гармонично созданные отношения — пропорции. Вот мы и подошли к тому ключевому слову, которое и определяет красоту во всем, что нас окружает, а точнее одну из очень важных составляющих, разлитую во вселенной, данную нам свыше.

Человек, пытаясь творить и создавать что-то своими руками, понял, как трудно создать что-то эстетичное и красивое.

Изучая окружающий мир в человеческом сознании стали проявляться геометрические фигуры – символы, которые и стали определяющими. Изучая небо, человек видел солнце и планеты, идущие по кругу. Смена времен года определяла кругооборот в природе. Что это как не круг. Круг – это одна из первых фигур осознанных человеком. К этому пришел еще в V веке до нашей эры Пифагор, а до него, видимо, за две тысячи лет пришли к этому иудеи. Ведь еще Авраам говорил, что мир круглый, как мяч, а люди на другой стороне земли ходят по отношению к нам наоборот.

Передвигаясь по земле, странствуя по свету, человек видел величественные горы, упирающиеся пирамидальными вершинами в небо. В сознании родилось другое понятие, другая геометрическая форма — треугольник. Это первая фигура, образующая замкнутую плоскую геометрическую фигуру. Египтяне использовали треугольник со сторонами 3*4*5 для построения прямого угла, используя для этого веревку с узелками. Треугольник имеет три стороны, а также указывает на начало, середину и конец, чего бы то ни было. Любой объемная форма также определяется тремя параметрами – это длина, ширина, высота. Ну и конечно это триединство.

Строя свое жилище, человек пришел к мысли, что лучше всего состыковывать прямоугольные камни или кирпичи. Это прямоугольник, а прямоугольник с одинаковыми сторонами это квадрат, имеющий 4 вершины. Квадрат — это следующая геометрическая форма, лежащая в основе всего устойчивого и основательного. Это 4 стихии, четыре элемента мироздания – огонь, вода, земля и воздух.

Наблюдая излучины рек, полеты птиц, равнины переходящие в пологие холмы, человек видел кривые линии, состоящие из дуг. Дуга это последующая, очень важная составляющая геометрической формы.

Ну и конечно, не надо забывать, что есть и прямая линия, у которой есть начало и есть видимый (воображаемый) конец. Мы видим её, смотря на линию горизонта, когда идет дождь и струи дождя падают вниз, дорога, уходящая за горизонт. Пуская стрелу в цель, охотник стремился пустить её с наибольшей силой по прямой, чтобы попасть в цель.

Вот основные формы, которые и определили, основополагающие законы построения форм.
Рассмотрим основные плоскостные построения пропорций.
Итак, одна из основополагающих компонентов при определении пропорций и соразмерностей служат построения при помощи геометрических фигур и их взаимосвязи.

Глава 1 -Построение примитивов

 

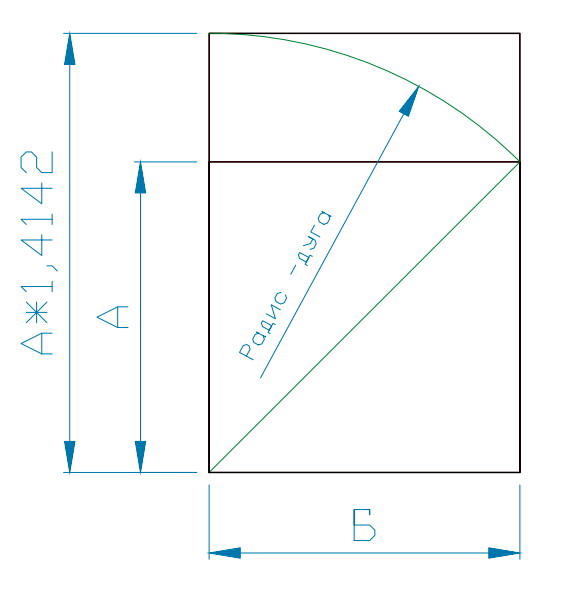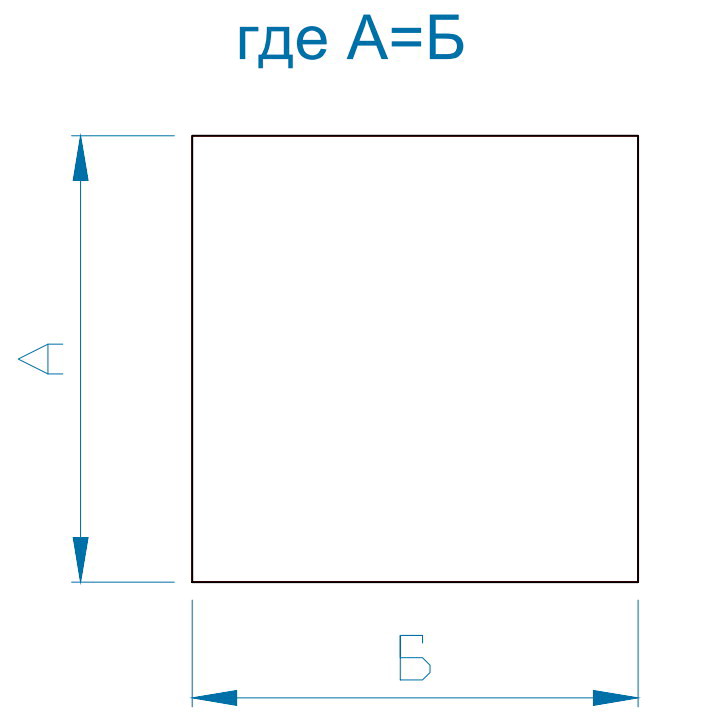
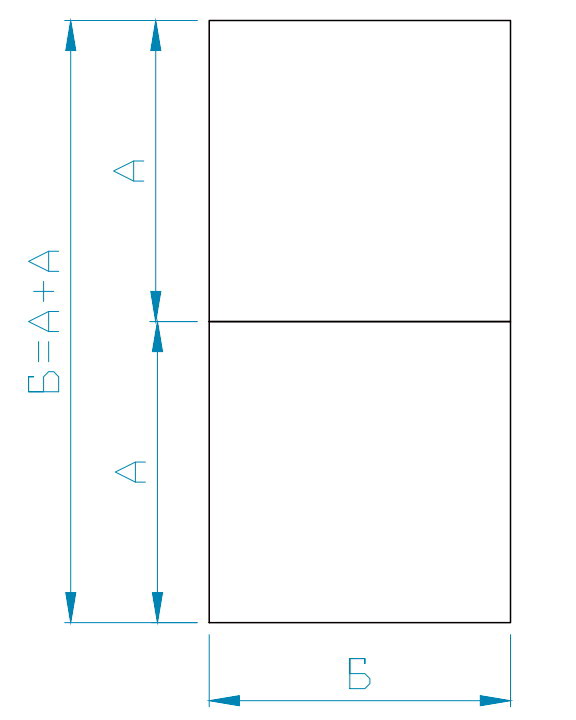
Рис 1 — квадрат	Рис 2 — прямоугольник из 2-х квадратов	Рис 3 Прямоугольник из ув квадрата и диагонали

Более сложные пропорции происходят с более тонкими настройками пропорций, числовым рядом (функциями)соотношения сторон.
Например, стороны могут соотноситься 1:3; 1:4, 1:5 и т.д. или по функции сложения.
Например: 1:2; 2:3; 3:5; 5:8; 8:13 и т.д.

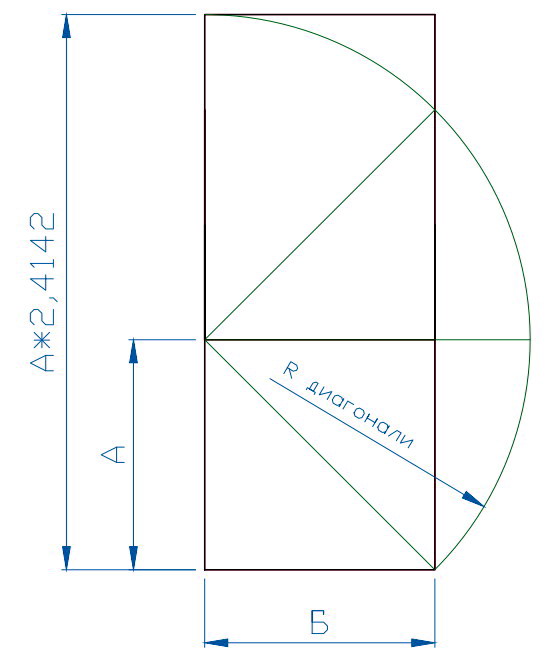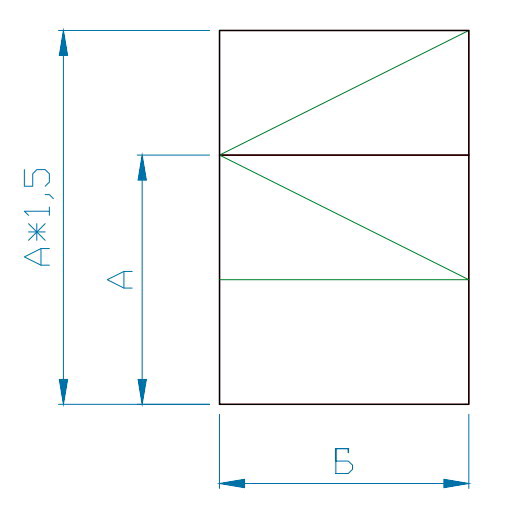
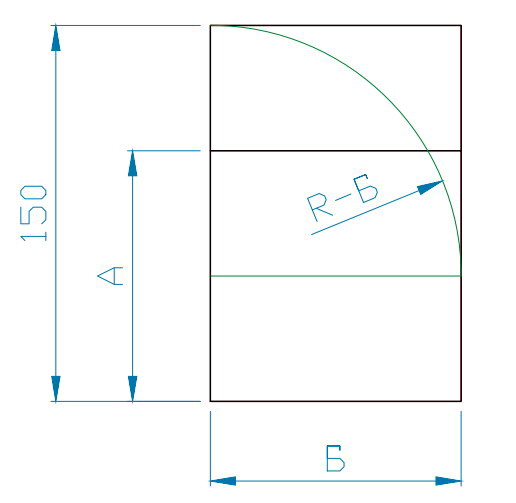
Рис 4 -Прямоугольник 1:1,5	Рис 5 -прямоугольник 1:1,5	Рис 6 -квадрат + диагональ

При построении этих фигур и изучая получившиеся пропорции, можно увидеть образовавшиеся треугольники — как равносторонние, равнобедренные, так и с образованием одновременно острого и тупого углов.

 

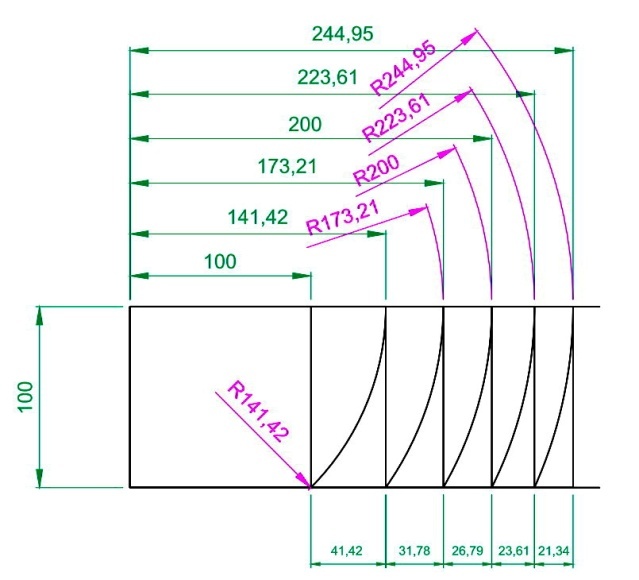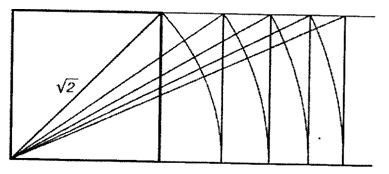
Рис 7 -Диагонали квадрата	Рис 8 -Построение из радиусов

Диагональ квадрата равна √2 (корень из 2 -1,4142). Диагональ из прямоугольника состоящего из двух квадратов – это √3 (корень из 3-1,732); следующая диагональ – это √4 (корень из 4- 2,0); следующая диагональ – это √5 (корень из 5 – 2,236) и т.д.

Глава 2 Числа и их числовые значения

Чтобы перейти числовым выражениям пропорций и их соотношений, необходимо понять, что обозначает каждое из чисел, какой оно несет информационный смысл. Изучая числа и их значения можно найти много интересного. Изучением чисел их смыслом и таинственными знаками люди занимались издревле.

Характеристика чисел и их выражение:

Число 1 (Единица) – это число мудрости «монада», или многообразие, сведенное к единству.

Единица – это первопричина, сотворение, вселенная, солнце. Единица — основа всего, основа жизни, это прямая связь земли и космоса, основа двух начал света и тьмы.

Число 2 (Два) – это две части целого, мужское начало и женское, инь и янь, черное и белое, свет и тьма. Дуализм этого число на низком уровне – это борьба двух противоположностей – добра и зла, на высоком уровне – это тесный союз, земли и солнца, мужчины и женщины, земли и воды. Это двойственное начало, в целом, олицетворяет сотворение Сущего, разделение на свет и тьму, на твердь и воду. Это основание любой прямоугольной формы или отрезка.

Число 3 (Три) – это синтез, результат рождения нового. В геометрии это треугольник, первая фигура, производящая множественную структуру бесконечности. Это число даёт начало середину и конец . Трис-мегист греческое слово, обозначающее трижды великий. В Православии оно неразрывно связано со Святой Троицей — триединством. Это первое число гармонии — Трио, которое стремится к покою.

Число 4 (Четыре)- это первое геометрическое тело, образующее геометрическое тело в плоскости и имеющее систему координат. Это четыре стороны света, четыре времени года, четыре периода жизни человека. Пифагорейцы называли его корнем всех вещей. Это основа, столп, характеризуется полным покоем, формой не стремящейся никуда. Квадра -полный покой , вот его основа и устойчивое движение.

Число 5 (Пять) – это число, обозначает победу духовного над материальным. Попытка выйти из пределов примитивного числа 4, это число Гуру, высшего учительства. Число пять – Квинта — обозначает анархию, подъем над порядком, вечное движение и стремление к высшему началу.

Число 5 также указывает на пять органов чувств, которыми обладает человек. Фигура человека с раскинутыми руками и расставленными ногами вписывается в пятиконечную звезду, звезду магов. Это является символом человеческого существа как микрокосмоса во вселенной.

Число 6 (Шесть) – это вложенные друг в друга треугольники, образующие гексаграмму – шестиконечную звезду. Один треугольник обращен вершиной вверх – это прямое воплощение триединства божественного начала, другой треугольник обращен вершиной вниз – его тень, мир явлений, загробный мир, мир душ. Шестиконечная звезда считается талисманом величайшего Иудейского царя Шломо (Саломона), а до этого была звездой Давида. Соответствует дому Девы. Это устойчивая геометрическая форма – Секста — с двумя началами, стремящаяся к повторению. Пчелиные соты, состоящие из шестиугольника – это лучшее тому подтверждение. Число шесть символизирует гармонию, некое равновесие, которое стремится к расширению и повторению, и составляет сумму первых трех простых чисел (1+2+3=6). Это четное число и по китайскому календарю это ИНЬ, обозначает женскую энергию, подчиненную мужскому началу ЯНЬ. Это число обозначает материальный мир, там, где правит женщина, привнося в дом тепло и уют. В библии говорится, что Бог создал человека на шестой день. Это число указывает на баланс духовного и материального, на вечное и преходящее (как говорили Пифагорейцы, а потом и Аристотель).

Число 7 (Семь) – это особое мистическое число, связанное с кругооборотом. Семь дней недели, из которых шесть дней Бог творил, а на седьмой день – отдыхал. Число 7 – это некая медитация, созерцание, того, что сделано, осмысление, уход от мирской суеты. Это число характеризует собой единство неба и земли. Это число управляет магическими силами: стены Иерихона рухнули, после того, как израильтяне обошли вокруг них 7 раз. В числовом формате, это число нельзя получить путем перемножения других чисел. Число семь также соотносится с семью основными цветами, и с 7 нотами в музыке – а это уже гармония вселенной. Оно связано и с Луной, и её циклами – 4 недели по семь дней.

Число 8 (Восемь) – это число единства земли и материи. Это удвоение числа 4, расширения материи, построения вселенной. Это связь земли и неба, петля Мёбиуса – олицетворяющая бесконечность. С одной стороны это новые планы, новые проекты, с другой стороны это сильные падения. С числом восемь связаны представления о жизни после смерти, о появлении нового духовного начала. Число 8 связано и трехмерной фигурой, такой как куб.

Число 9 (Девять) – это первое число ограничения всех начальных чисел, от 1 до 9. Это первый квадрат числа 3 (3 х 3 =9). Число высшего начала, стремящегося, однако, к низшему, к земле. При этом, число девять – это число перехода на новый уровень, число духовности и интеллекта.

Число 10 (Десять) – это совершенное число, первое созданное из соединения двух чисел 1 и 0.

Это число обозначает закон, и состоит из перемножения числа 2 и 5, является началом и объединением всех начал. Это число характеризует самодостаточность, и характеризуется тем фактом, что в окружности 360 градусов, а числа 3+6+0 в сумме образуют число 9. К тому же, если какое-то простое число умножить на 9 и произвести арифметический расчет, то всегда будет получаться число 9. (Например: 3х9=27, а 2+7=9 и т.д.).

Существую и сложные числа, такие как 11, 12 и т.д., но это уже отдельная история.

Глава 3 — построение звезд и многоугольников

Построение пиктограммы с пятью лучами.

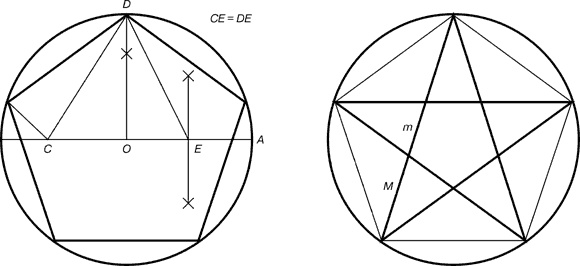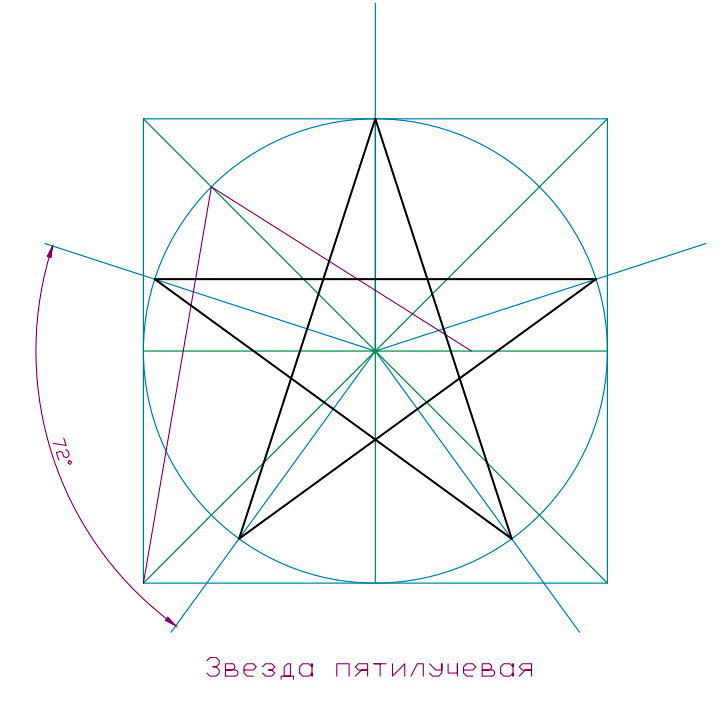
Рис 9	Рис 10

Многоугольник с пятью сторонами – пятиконечная звезда, это первое из сложных тел, которое идет за квадратом. Вершины пятиугольника вписываются в круг и имеют между собой угол равный 72˚. Пример построения показан на рисунке.

Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471…1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

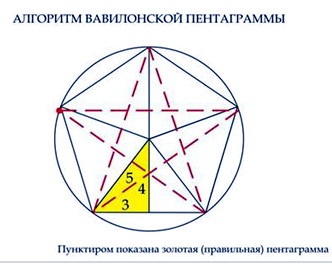
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

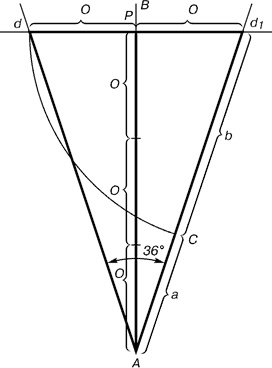
Рис 11	Рис 12

Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.

В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками.
Но золотой треугольник весьма близок к священному египетскому треугольнику
5-4-3, на котором строилась древнейшая «вавилонская» (неправильная) пентаграмма. Кто из древних и когда превратил «вавилонскую» пентаграмму в золотую, мы пока не знаем.

Рис 13 -Шести лучевая звезда	Рис 14 -Сота шестиугольник

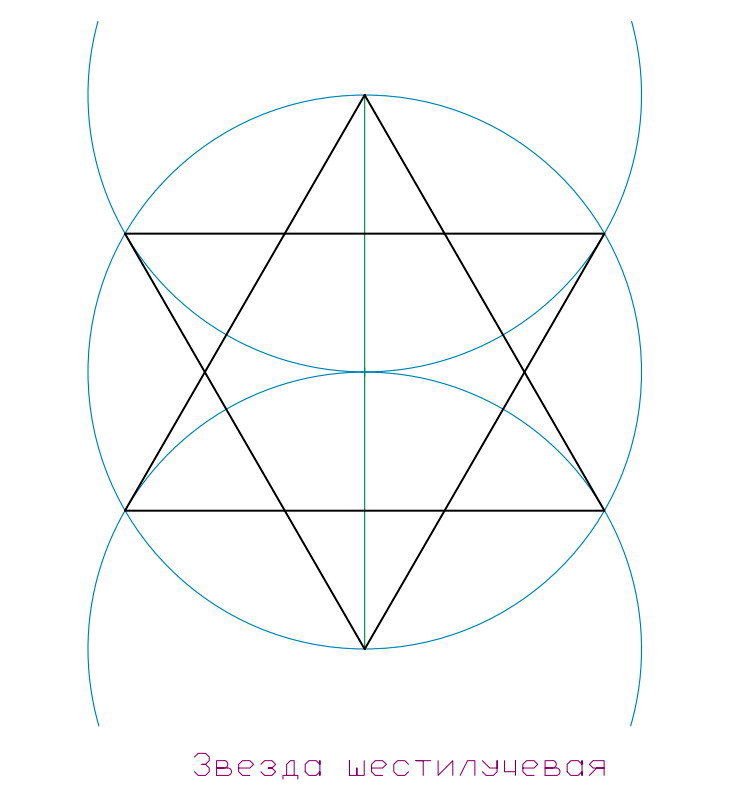
Шестиугольник или звезда с шестью лучами – это сложная форма, состоящая из двух треугольников, вписанных в круг. Вершины между собой имеют угол 60˚. При её построении, необходимо провести радиус из верхней и нижней вершин, и на окружности они образуют дополнительные точки построения шестиугольника. Треугольник, обращенный вершиной вверх – это духовная энергия, и обращен он к раю, треугольник обращенный вершиной вниз – это наше мирское тело, и обращен он к аду. Здесь проявляется единство и борьба противоположностей.

Звезда с шестью лучами являлась символом и была на щите царя Давида (а потом и Соломона).

Рис 15	Рис 16

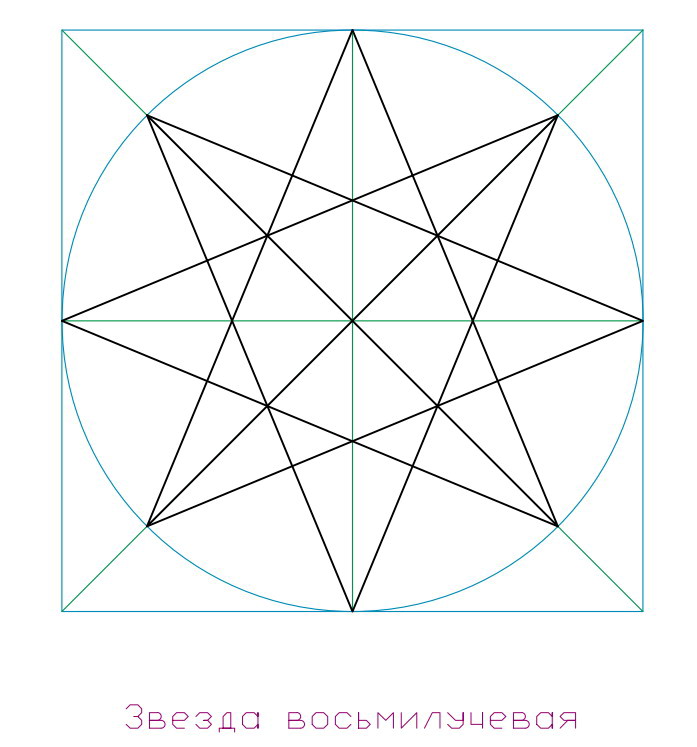
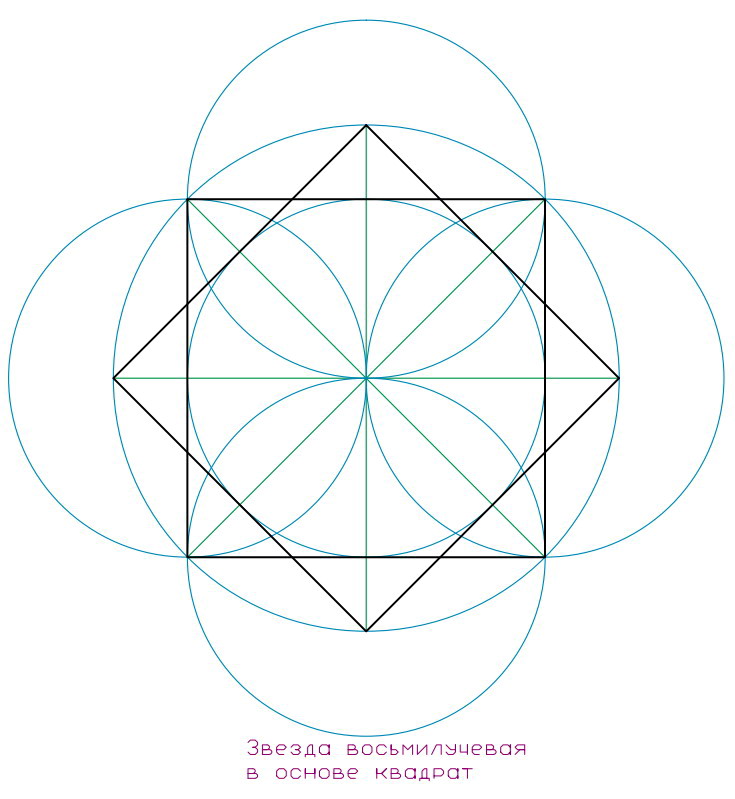
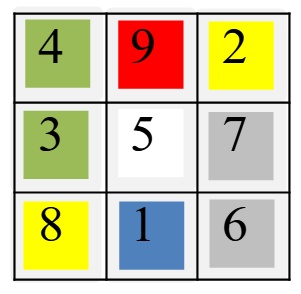
Восьми угольник или восьми лучевая звезда – это устойчивая форма с двумя квадратами, вписанными в круг, повернутыми по отношению друг к другу на 45˚. Восьми угольник очень любим восточными культурами, особенно почитался в Китае и Японии. На восьмиугольнике построен фэн-шуй, к нему относятся стихии (их 8)и знаки животных, окружающих человека (их четыре): это черепаха, тигр, феникс и дракон. Стихии это: огонь – вода; металл –дерево; почва+ — почва -. Восемь сторон света: это юг — юго-запад — запад — северо-запад – север – северо-восток – восток – юго-восток. Магический квадрат имеет магическое соотношение цифр: сумма цифр в каждой строке , столбце или диагонали составляет число 15. В Китае он назывался восьмиугольником Ба-гуа и определялся по сторонам света цветам и животным.

Рис 17	Рис 18	Рис 18

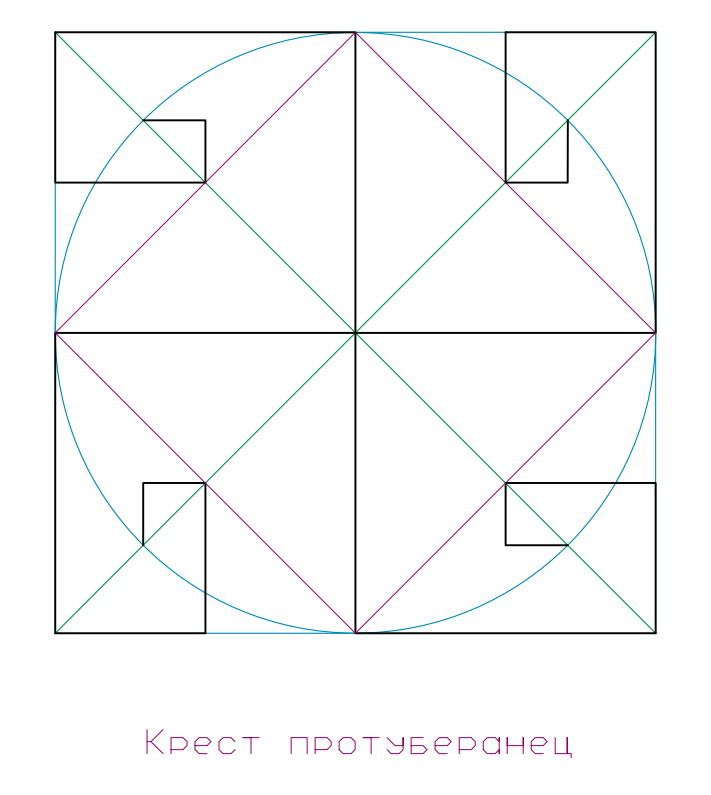
Квадрига креста Рис. 15 или танцующий в четырех стихиях крест, образуется при построении квадрата и круга. Это знак движения стихий.
Звезда протуберанец – это звезда с 8 вершинами, вписанными в круг.
Угол между вершинами будет — 45˚.
Может рисоваться и с 9 вершинами, тогда угол между вершинами будет создаваться 40˚.
Этот знак был распространен в Тибете и древней Индии.

Семиугольник – это одна из величайших форм природы.

Принципы мировой гармонии определены простыми геометрическими фигурами, одной из которых является семиугольник и семиугольная геометрическая сеть линий, которая получается в результате соединения вершин семиугольника линиями.
«Данную семиугольную сеть линий можно называть: гептагональная сеть (септагональная), и можно утверждать, что гептагональная сеть является наиболее значительной фигурой, которая определяет гармонические пропорции окружающего мира». С.Л.Панфилов

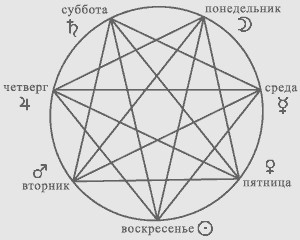Рис 19	Рис 20 -Астрологический семиугольник камней

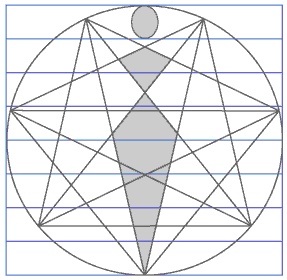
В том числе гептагональная сеть является фигурой, которая определяет основополагающие пропорции человеческого тела, что показано на рисунке:19

Тёмные контуры на рисунке показывают идеальную человеческую фигуру, которая вписана в линиях гептагональной сети.

Согласно древнегреческому скульптурному канону рост человеческого тела делится на 8 частей и величина головы составляет 1/8 часть от роста тела, что показано на рисунке синими линиями. Хотя в действительности согласно среднестатистическим антропометрическим размерам величина головы составляет 1/8 часть, если рост человека 180 сантиметров, но если рост человека 175 сантиметров, то величина головы составляет 1/7,5 часть, или если рост человека 170 сантиметров, то величина головы составляет приблизительно 1/7 часть. Но всё же считается, что идеальная величина головы соответствует греческому скульптурному канону.

В числе многих объектов мира наиболее значительным памятником человеческих знаний являются Египетские Пирамиды, и в частности пирамида Хеопса.
Согласно разным источникам основными размерами пирамиды Хеопса являются: длина стороны основания 500 локтей, высота 318 локтей, угол наклона боковых граней 51 градус 50 минут.

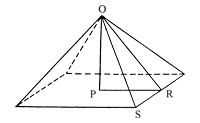
Согласно перечисленным размерам главные пропорции пирамиды Хеопса заключаются в соотношениях линий треугольника, который образован высотой ОР, половиной длины основания PR и апофемой (длиной боковой грани) OR, что показано на рисунке:

Рис.22

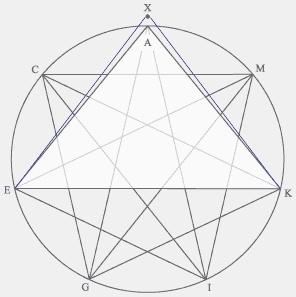Рис 21	Рис 22

В соотношениях линий OR/PR зашифрована величина золотого сечения, а в соотношениях линий PR/PO зашифровано число «пи».
Угол PRO с вершиной в точке R является углом наклона боковых граней, а угол PSO с вершиной в точке S является углом наклона диагональных ребер.
Угол наклона боковых граней и угол наклона диагональных рёбер пирамиды имеют разную величину.
Угол PRO и угол PSO являются основными параметрами, которые позволяют сопоставить пропорции пирамиды с пропорциями семиугольника.
Из исторической справки: « среди прочих знамений пирамиды Хеопса, и содержащееся в ее пропорциях золотое сечение. На упоминаемой странице http://bullbear.msm/ru/rus/fr_main513.htm находим: «Длина грани пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды — 484.4 фута (147.6 м). Длина грани, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) — это числа из последовательности Фибоначчи.»

Многие исследователи Пирамиды Хеопса предполагают, что строителям Египетских Пирамид были известны число золотого сечения и число «пи», а также предполагают, что эти золотые числа были ключевыми в проекте пирамид, но в действительности знание этих чисел не является необходимым, поскольку для строительства пирамид достаточно знать пропорции семиугольника и использовать соотношения линий, которые существуют в геометрической фигуре семиугольника, что показано на следующем рисунке:

На рис. 22 треугольник АЕК является приблизительным силуэтом боковых граней пирамиды Хеопса.
Показанный силуэт боковых граней является приблизительным, поскольку угол семиугольника ЕКА с вершиной в точке К имеет величину 360/7=51,429 градусов (51 градус 25,71 минут), а угол наклона граней пирамиды имеет величину 51 градус 50 минут.
Эту разницу строители компенсировали добавлением к высоте треугольника АЕК величины человеческого роста АХ. То есть строители пирамиды Хеопса поместили в вершине треугольника и условно поместили на вершине пирамиды фигуру человека, и в результате получили угол ЕКХ с вершиной в точке К равный 51 градус 50 минут.
А именно если высота треугольника ЕКХ 318 локтей, то высота треугольника ЕКА приблизительно 314 локтей, а высота человеческого роста приблизительно 4 локтя.
Строители пирамиды Хеопса увеличили правильный угол семиугольника, будто бы на вершине пирамиды находится человек, и в результате в соотношениях линий ЕК/КХ было зашифровано число золотого сечения, а в пропорциях пирамиды были заложены пропорции человеческого тела, что было проектом будущей пирамиды.
По существу строители пирамиды Хеопса вписали семиугольную сеть линий в живую окружность, в которой величина вертикального диаметра отличалась от величины горизонтального диаметра относительной величиной человеческого роста.

Основной мерой измерения в древнем Египте был локоть, который состоял из семи ладоней, а каждая ладонь подразделялась на четыре пальца. Итого локоть состоял из 28 пальцев, что соответствовало 28 дням лунного месяца.
Обратите внимание, что бигептагональная сеть линий имеет 14 вершин, а квадрагептагональная сеть линий имеет 28 вершин, что также равно числу дней лунного месяца.

В современной египтологии известны разные параметры египетского локтя:
— простой египетский локоть = 6 ладоней = 24 пальца = 450 миллиметров;
— королевский египетский локоть = 7 ладоней = 28 пальцев = 525 миллиметров.
Но всё же величина 466 миллиметров является наиболее достоверной, поскольку это антропометрическая величина человеческого локтя.

Глава 4 -принципы золотого сечения

Поиск наилучших взаимоотношений и сочетаний привел к нахождению идеальных пропорция. В древности его называли Божественными пропорциями.

Еще в Древнем Египте за единицу измерения тела принимали длину стопы, в более поздние времена — длину среднего пальца руки. Были найдены и абсолютные сочетания при построении архитектуры 3:4:5.

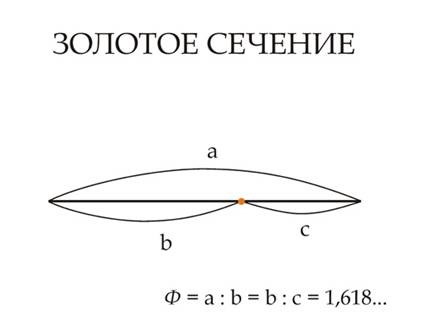
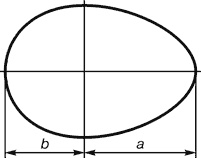
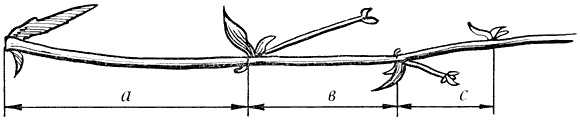
Основа золотого сечения, заложенная ещё с Евклида, означает пропорциональное соотношение частей: большая часть относится к средней, как средняя к меньшей, или если записать это формулой: a:b=b:c или c:b=b:a

Рис 23	Рис 24

Золотое сечении — соотношение пропорций, при котором целое так относится к своей большей части, как большая к меньшей. (Если обозначить целое как С, большую часть А, меньшую В, то правило золотого сечения выступает как соотношение С:А=А:В.) Автор золотого правила — Пифагор — считал совершенным такое тело, в котором расстояние от темени до пояса относилось к обшей длине тела как 1:3. Отклонения величины веса и объема тела от идеальных норм зависят прежде всего от строения скелета. Важно, чтобы тело было пропорционально.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Золотое сечении — соотношение пропорций, при котором целое так относится к своей большей части, как большая к меньшей. (Если обозначить целое как С, большую часть А, меньшую В, то правило золотого сечения выступает как соотношение С:А=А:В.) Автор золотого правила — Пифагор — считал совершенным такое тело, в котором расстояние от темени до пояса относилось к обшей длине тела как 1:3. Отклонения величины веса и объема тела от идеальных норм зависят прежде всего от строения скелета. Важно, чтобы тело было пропорционально.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Канон — система идеальных пропорций человеческого тела — была разработана древнегреческим скульптором Поликлетом в V веке до нашей эры. Ваятель попытался научно, точно определить пропорции человеческого тела, согласно с его представлениями об идеале. В соответствии с эстетическим каноном греческого скульптора Поликлета единицей измерения тела служила голова; длина тела должна быть равной восьми размерам головы.

(Polэkleitos) из Аргоса, древнегреческий скульптор и теоретик искусства второй половины V в. до н. э. Один из ведущих представителей высокой классики. Работал в Аргосе. Творчеству Поликлета свойственно тяготение к художественной нормативности, которое выразилось в его сочинении «Канон» (сохранилось 2 фрагмента). Под влиянием учения Пифагора Поликлет стремился математически обосновать и воплотить идеальные пропорциональные отношения человеческой фигуры, создать возвышенный гармонический образ человека — гражданина полиса. Статуи Поликлета («Дорифор». или «Копьеносец», около 440 до н. э.: «Раненая амазонка», около 440-430 до н. э.; «Диадумен», около 420-10 до н. э.). выполненные преимущественно в бронзе, утрачены и известны по римским копиям и свидетельствам античных авторов. Несколько тяжеловатые по пропорциям, исполненные внешнего покоя и скрытой внутренней динамики, они построены на принципе взаимоуравновешивающего перекрёстного движения различных частей тела (так называемых хиазм): поднятому плечу соответствует опущенное бедро (и наоборот). Совершенство, обобщённость и классическая ясность пластики сочетаются в них со свободной непринуждённостью композиции.

«Успех художественного произведения, — утверждал Поликлет, — получается от многих числовых отношений, причем любая мелочь может его нарушить». Свой идеал атлета-гражданина Поликлет воплотил в бронзовой скульптуре юноши с копьем, отлитой около 450—440 годов до н. э. Могучий обнаженный атлет — Дорифор («Копьеносец») — изображен в спокойной и величественной позе. Он держит в руке копье, которое лежит на левом плече, и слетка повернув голову, смотрит в даль. Кажется, что юноша только что нагнул вперед и остановился.  Красота человека становится для нею мерой ценности разумно устроенною мира.

Вот результаты его вычислений: голова — 1/7 всего роста, лицо и кисть руки — 1/10, ступня -1/6. Однако уже современникам фигуры Поликлета показались слишком массивными, «квадратными». Тем не менее, каноны стали нормой для античности и с некоторыми изменениями для художников ренессанса и классицизма. Практически канон Поликлета был воплощен им в статуе Дорифор («Копьеносец»). Широкие плечи почти равны высоте туловища, половина высоты тела приходится на лонное сращение, высота головы восемь раз укладывается по высоте тела, а центр «золотой пропорции» приходится на уровень пупка.

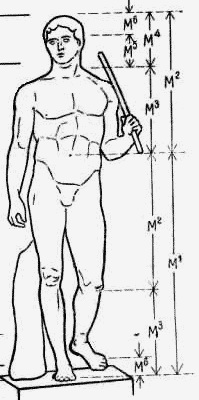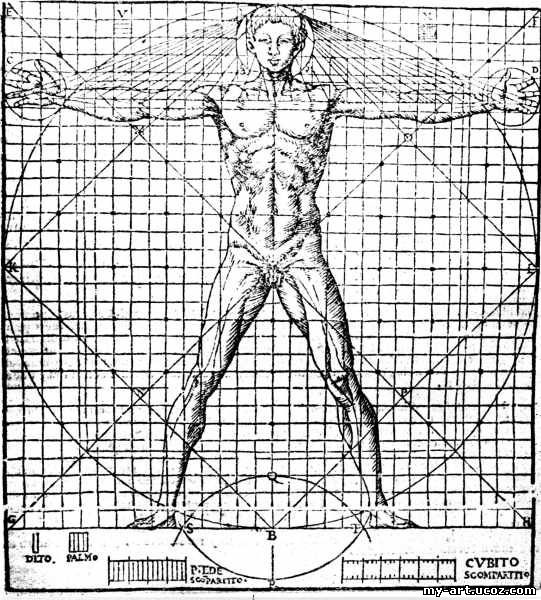
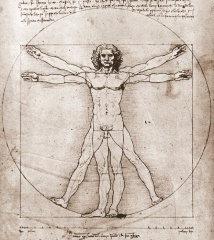
Рис 25-Пропорции Поликлета	Рис — 26-Пропорции Леонардо	Рис 27—Пропорции Дорифора

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Древнеримский архитектор Витрувий — его работы были возвращены к жизни основателями Возрождения — настаивал на том, чтобы храмы строились в соответствии с пропорциями человеческого тела. К таким пропорциям относится не только золотое сечение, но и экстраполяция кругов и квадратов, описанных вокруг фигуры стоящего человека с расставленными в стороны руками и ногами.

Знаменитый рисунок этой фигуры, созданный примерно в 1490г. — его часто называют «Человек как микрокосм» — можно найти в тетрадях Леонардо.

Пропорции фигур у Античных скульпторов.
В создании своих творений греческие мастера (Фидий, Мирон, Пракситель и др.) использовали этот принцип золотой пропорции. Центр золотой пропорции строения человеческого тела располагался точно в месте пупка (это не так пр. автора).

Рис 28 Фигура Дорифора (Поликлет)	Рис 29	Рис 30 Фигура юноши из Аргоса

Мирон большую часть своей жизни работал в Афинах, расцвет его творчества падает на вторую четверть V века до н. э.

Среди его произведений наибольшей известностью пользовалась статуя «Дискобол», исполненная между 460 и 450 годами до н. э. Она прославляет победителя атлетических состязаний. Сжав диск в правой руке, обнаженный юноша наклонился вперед. Рука с диском отведена назад до предела. Кажется, через мгновение атлет распрямится и брошенный с огромной силой диск полетит на далекое расстояние. Все тело юноши пронизано захватившим его движением.

Впились в землю пальцы правой ноги, которая служит опорой телу, резко обозначились напряженные мускулы, и, словно тугой лук, согнуты руки. Новаторство Мирона заключалось в том, что он одним из первых мастеров греческого искусства сумел передать в скульптуре ощущение движения. В позе «Дискобола» как бы слиты несколько последовательных движений: размах, мгновенная остановка перед броском и намек на сам бросок. Эта поза не является точным повторением какого-то одного момента в движении атлета. Правдивое впечатление движения в искусстве Мирона складывается благодаря единству простых и легко воспринимаемых жестов, которые передают различные моменты реально движущейся фигуры.

Фигура «Дискобола» передает огромное внутреннее напряжение, которое сдержано внешними формами скульптуры, упругими замкнутыми линиями, очерчивающими ее силуэт. В образе атлета Мирон раскрывает способность человека к активному действию.

Впоследствии это изображение было дополнено Агриппой и Фладдом, которые запечатлели его в космическом контексте — в зодиакальном круге с нанесенными на нем соответствующими астрологическими знаками. Таким образом, вечные «гармонические пропорции» всей Вселенной проявлялись как внутренне присущие чуду человеческого тела, в микрокосме которого воплощалось божественное совершенство макрокосма.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Рис 31 -Мирон. Дискобол	Рис 32 -Раненая Амазонка	Рис 32

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Древнеримский архитектор Витрувий — его работы были возвращены к жизни основателями Возрождения — настаивал на том, чтобы храмы строились в соответствии с пропорциями человеческого тела. К таким пропорциям относится не только золотое сечение, но и экстраполяция кругов и квадратов, описанных вокруг фигуры стоящего человека с расставленными в стороны руками и ногами.

Знаменитый рисунок этой фигуры, созданный примерно в 1490г. — его часто называют «Человек как микрокосм» — можно найти в тетрадях Леонардо.

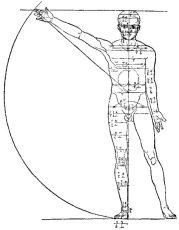
Альбрехт Дюрер ( Albrecht Durer ). Теоретик искусства. Автор трудов: «Руководство к измерению с помощью циркуля и линейки» (Нюрнберг, 1525); «Четыре книги о пропорциях человека» (Нюрнберг, 1528).

Классик немецкого Возрождения, Альбрехт Дюрер (1471-1528) работая над гравюрой «Немезида или Большая Фортуна» (Ок. 1501) применил принципы пропорционирования Витрувия. Согласно исследованию Эрвина Панофского (1892-1968), признанного корифея европейского искусствоведения, в изображённой фигуре даже размер большого пальца согласуется с Витрувием. Но результат оказался очень далёк от классического идеала и не производил желаемого впечатления, в том числе и на самого Дюрера. В дальнейшем своём творчестве

Альбрехт Дюрер от услуг Витрувия отказался, но им самим был написан трактат альтернативный труду Витрувия, полное название которого звучит так: «Здесь заключены четыре книги о пропорциях человеческого тела, найденных и описанных Альбрехтом Дюрером из Нюрнберга на пользу всем любящим таковую науку». В начале трактата Дюрер, критически осмысливший наследие Витрувия, заявляет: «…только совсем слабый разум не верит, что он может найти нечто новое, но держится всегда старого пути, следуя за другими и никогда не осмеливаясь самостоятельно думать».

Дерзость у Дюрера сочетается со скромностью, о которой он напоминает людям говоря: «Нет также на земле человека, который мог бы окончательно сказать, какою должна быть прекраснейшая человеческая фигура. Никто не знает этого, кроме одного Бога».

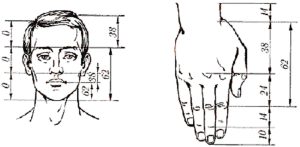Рис 33	Рис 34

Лука Пачоли, предложил формулы золотых пропорций:

Рис 35

Пачоли писал: «…подобно тому, как Бог не может быть ни определен, ни словом разъяснен, наша пропорция не может быть выражена ни доступным нам числом, ни какой бы то ни было рациональной величиной и остается скрытой и тайной и поэтому математиками названа иррациональной».
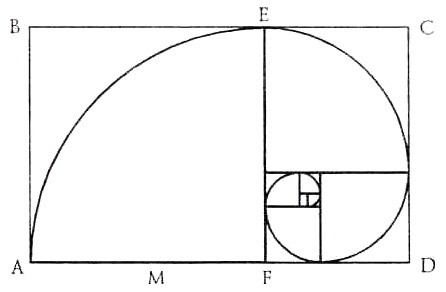
Золотая логарифмическая спираль

Рис 36	Рис 37

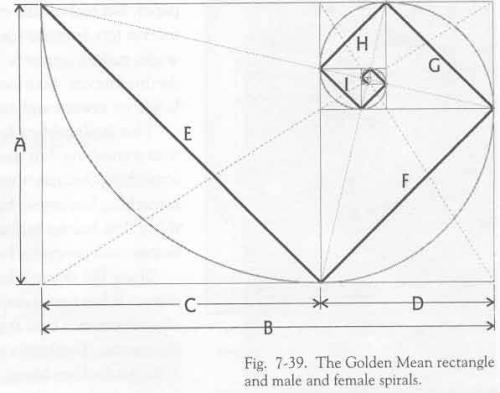
Что общего у расположения полипептидных цепей нуклеиновых кислот, лепестков розы, раковин моллюсков, рогов млекопитающих, и далеких космических галактик?

Ответ известен: структура, основанная на логарифмической спирали. Т. Кук открыл роль золотой логарифмической спирали в строении растительных и животных объектах, доказав что феномен роста в биологических объектах связан со спиралями золотого сечения.

Что такое золотая логарифмическая спираль? В ее основе золотой прямоугольник: Последовательно отрезая от него квадраты и вписывая в каждый по четверти окружности, мы и получаем золотую логарифмическую спираль.

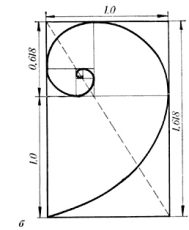Рис  38 Спираль Архимеда	Рис 39

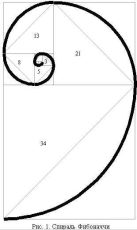
Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

Дело в том, что сначала были «открыты» числа натуральные; затем их отношения – числа рациональные. И лишь позже – после открытия пифагорийцами несоизмеримых отрезков – на свет появились иррациональные числа. Скажем, в десятичной, пятеричной, двоичной и других классических позиционных системах счисления в качестве своеобразной первоосновы были выбраны натуральные числа – 10, 5, 2, – из которых уже по определенным правилам конструировались все другие натуральные, а также рациональные и иррациональные числа.

Своего рода альтернативой существующим способам счисления выступает новая, иррациональная система, в качестве первоосновы, начала счисления которой выбрано иррациональное число (являющееся, напомним, корнем уравнения золотого сечения); через него уже выражаются другие действительные числа.

В такой системе счисления любое натуральное число всегда представимо в виде конечной – а не бесконечной, как думали ранее! – суммы степеней любой из золотых S-пропорций. Это одна из причин, почему «иррациональная» арифметика, обладая удивительной математической простотой и изяществом, как бы вобрала в себя лучшие качества классической двоичной и «Фибоначчиевой» арифметики.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).
Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).
(Андрей Чернов. Заметки о вечном. SECTIO AUREA. ИМЯ, ДАННОЕ ПО ОШИБКЕ)

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи). Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится».

Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр

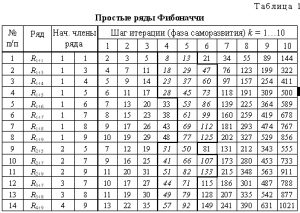
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему. Основная идея состоит в том, что каждое последующее число равно сумме двух предыдущих чисел. К примеру: 3 является суммой 1+2; 5 является суммой 3+2 и т.д.

Однако, надо отдать должное, этот числовой ряд был известен еще в трудах древних Индийских ученых.

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…

Фибоначчи также известен тем, что стал использовать в бухгалтерии арабские числа и сего легкой руки они закрепились в Европе.

Рис 40	Рис 41

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Первые работы, специально посвященные золотому сечению, вышли в конце XVIII столетия. А в середине XIX века немецкий профессор издал Адольф Цейзинг капитальное «Новое учение о пропорциях тела человека, из остающихся до сих пор непознанных морфологических основ, пронизывающих всю природу и искусство». В 1855 г. труд Цейзинга был переиздан под названием «Эстетические исследования».

Цейзинг считал, что все в мире можно объяснить золотой пропорцией и рассматривал ее в качестве основного морфологического закона природы и искусства. Он сам сделал тысячи обмеров и показал, что этот закон работает и в пропорциях тела человека и в телах «красивых животных».

Более подробно мы рассмотрим это далее на различных примерах.

Построения сложных геометрических тел и их пропорции

При построении сложных геометрических и архитектурных тел необходимо находить пропорции и числовые порядки, объединенные в закономерности.

Покажем наглядно некоторые примеры различных пропорций и их закономерностей.

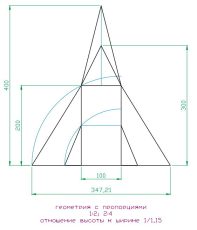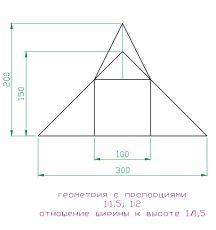
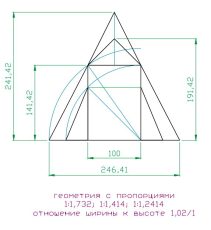
Рис 42	Рис 43	Рис 44

Этот пример на основе треугольников и прямоугольника наглядно показывает, насколько изменяются пропорции при изменении числовых взаимоотношений. Если на рисунке 42 форма выглядит приземлено, она прочно стоит на своем основании, т.к. основанием служит равнобедренный треугольник, то на рисунке 44 форма устремляется вверх, выглядит более динамичной, как ракета устремленное в небо.

Рис 45	Рис 46	Рис 47

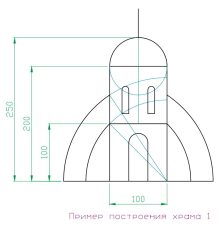
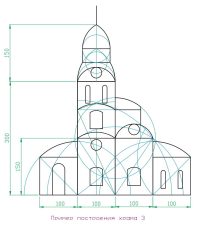
На этих рисунках показаны примеры условного построения храма при использовании определенных построений и пропорций.

Как можно увидеть форма, её эстетические и параметры восприятия сильно меняются при изменении пропорций. Эти приемы использовали архитекторы и строители на протяжении тысячелетий. При правильном использовании этих закономерностей можно усиливать те или иные свойства архитектуры: её динамику, устремленность или приземленность, плавность и гармоничность или готическую остроконечность. Эти свойства архитектуры мы более подробно рассмотрим позже. Архитекторы на протяжении многих веков применяли различные пропорции при строительстве архитектуры, которые выражали духовные устремления той эпохи.  Это отразилось в архитектуре в таких стилях Античность, Средневековье, Возрождение, Готика, Барокко и т.д.

Рассмотрим эти пропорции на основе храма Парфенона.
Золотое сечение было известно древним грекам. Вряд ли можно сомневаться в том, что некоторые древнегреческие архитекторы и скульпторы сознательно использовали его в своих творениях. Примером может служить храм Парфенона.

Рис 48	Рис 49	Рис 50

Главным зодчим храма Перикл назначил крупнейшего архитектора Греции Иктина, а его помощником — Калликрата. Строительство здания продолжалось девять лет, с 447 по 438 год до н. э. По своему плану Парфенон — дорический периптер размером 70×31 м, окруженный сорока шестью колоннами. Однако Иктин обогатил архитектуру храма многими элементами ионического ордера: вместо обычного шестиколонного портика на фасадах здания поставлены великолепные восьмиколонные портики; сами колонны высотой в 10.5 м стали более стройными, чем в предшествующих дорических храмах; наконец, для украшения Парфенона использован ионический фриз, сплошной лентой проходящий за колоннами по стене здания. При сооружении храмов на Акрополе архитекторы стремились к гармоническому сочетанию обоих ордеров, когда мужественная и строгая дорика согласовывалась с утонченной и грациозной ионикой. Главная точка зрения на Парфенон, на которую рассчитывали его создатели, — с угла, с северо-запада.

Впечатление безупречной красоты Парфенона возникает благодаря ясному чувству меры и гармонии, которые проявляются во всем облике храма. Все линии представляются глазу идеально правильными. На самом деле Парфенон построен с учетом особенностей человеческого зрения. Прямая линия стилобата, на котором возвышается здание, так же как и линия архитрава, в действительности изогнута в силу того, что идеальная прямая линия издали нам показалась бы слегка вогнутой. Чтобы избегнуть этого, строители сделали стилобат и ведущие к нему ступени в центре на 10 см выше, чем по краям. Угловые колонны Парфенона более массивны и ближе подвинуты к соседним, иначе при ярком свете они казались бы более тонкими. Измерения показали, что колонны слегка наклонены к центру здания, но кажутся строго вертикальными.

Расстояния между ними различны, хотя воспринимаются как одинаковые. Все это придает архитектурному облику Парфенона удивительную жизненность и неповторимую красоту. Внутри здание было разделено стеной на две неравные части. В главном помещении целле — стояла знаменитая статуя Афины-Парфенос (Афины-Девы), созданная Фидием в 447—438 годах до н. э. из золота и слоновой кости и мрамора, из которого был построен храм. В V веке н. э. статую Афины увез в Константинополь один иэ византийских императоров, и там спустя 10 лет она погибла при пожаре. Западную половину храма занимал зал с четырьмя ионическими колоннами — комната для девушек, где юные афинянки ткали священную одежду, которую жители юрода приносили в дар своей богине.

Там же хранились казна Афинского морского союза и государственный архив. Это помещение называли «Парфенон» от греческого слова «нарфенос» «дева». С IV века до н. э. название «Парфенон» стало относиться ко всему храму. О жизни и подвигах богини Афины, покровительницы города, связаны скульптурные украшения Парфенона, созданные Фидием совместно с его талантливыми учениками. В работе принял участие и целый ряд мастеров, чьи имена остались неизвестными. В процессе строительства храма, в 447—443 годах до н. э., были исполнены 92 метопы, а в 442—438 годах до н. э. — лента ионического фриза, проходящая за колоннами вокруг всего здания. В 432 году до н. э. мастера завершили работу над композициями фронтонов. Скульптурный ансамбль Парфенона — одно из величайших творений мирового искусства. Он отличался редкой художественной цельностью и логической завершенностью. Это воплощенная в мраморе ясная и величавая поэма, героиней которой стала Афина.

Совершенно иной Эрехейон.

В 421-405 годах до н. э. неподалеку от Парфенона в северной части холка воздвигли небольшой храм ионического ордера, посвященный Афине, Посейдону и мифическому царю Эрехгею. От его имени получило название Эрехион. В нем хранились древнейшие святыни. Эрехион стоят на месте, где в древности, согласно мифам, происходил спор Афины с Посейдоном. В полу храма было отверстие, через которое показывали след на скале, оставленный трезубцем Посейдона, а перед храмом росла священная маслина.

По-видимому, проект Эрехтейона был задуман еще при жизни Перикла и Фидия. Сооружая здание, строители должны были считаться со священными местами Акрополя. Особенность храма совершенно необычная планировка и асимметричное расположение помещений. Умело использовав неровности почвы, строители искусно подчинили композицию храма окружающему рельефу: восточная половина здания на 3 м выше западной. Три различных портика примыкают к храму. Стройные ионические колонны поддерживают два из них, в третьем крышу несут скульптурные изображения девушек, так называемые карпаиды.

Рис 51

Пропорции здания таковы, что у зрителя не возникает впечатления, будто ноша тяжела для девушек. Статуи органично согласованы с архитектурой: они выполняют конструктивную роль, заменяя колонны, и вместе с тем замечательно смотрятся на фоне мраморной стены храма. Девушки представлены в свободных позах, их одежды ниспадают богатыми складками. Кажется, что они медленно шествуют вперед, словно направляясь в сторону Парфенона. По контрасту с гордым величием Парфенона Эрехион радует глаз своей живописностью и декоративным изяществом.

Очень многие архитекторы обращались и обращаются к золотым пропорциям.
Например, архитектор Монферан при строительстве Исаакиевского собора сохранил все те же совершенные пропорции.

Рис 52

Числовые ряды, порядки, пропорции

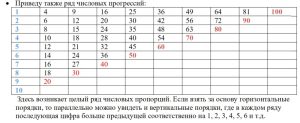
Обращая наш взгляд к числовым порядкам и отношениям, можно увидеть четкие закономерности, не всегда видимые с первого взгляда. Этих числовых порядков достаточно много и мы приведем лишь некоторые из них.

Порядок удвоения первого числа с суммой предыдущего. 1+1=2; 2+1=3; 3+2=5; 5+3=8; 8+5=13; 13+8=21 и т.д. Итак, получаем числовой ряд: _1_3_5_8_13_21_34_и т.д. Здесь можно отметить, что некоторые из них кратны 2, некоторые кратны 3, и многие числа сложные, т.е. не кратны ни одному из чисел (например 5 и 13).
Порядок удвоения суммы чисел: 1+1=2; 2+2=4; 4+4=8; 8+8=16; 16+16=32 и т.д.
Итак, получаем: _2_4_8_16_32_64_128_и т.д. Все цифры в этом порядке кратны 2.

Порядок увеличения суммы на три, т.е. кратно 3: 3; 3+3=6; 6+3=9; 9+3=12; 12+3=15; 15+3=18; 18+3=21 и т.д. Получаем: _3_6_9_12_15_18_21_
Порядок умножения последовательности чисел от 1 до 9 на 2: 1х2=2; 2х2=4; 3х2=6; 4х2=8; 5х2=10; 6х2=12; 7х2=14; 8х2=16; 9х2=19. Получаем: _2_4_6_8_10_12_14_16_18_ Здесь видна интересная закономерность – произведение последовательных чисел, умноженное на два. Кратно 2 и отличается от предыдущего на 2.
Порядок суммы последовательных пар чисел: 1+2=3; 3+4=7; 7+8=15; 15+16=31 или 1+2=3; 3+4=7; 5+6=11; 7+8=15; 9+10=19. Получаем: _1_3_7_11_15_19_
Последовательность, где сумма чисел равна одному из слагаемых и последующему за ним числу: 1+2=3; 2+3=5; 3+4=7; 4+5=9; 5+6=11; 6+7=13; 7+8=15; 8+9=17; 9+10=19 и т.д. Получаем: _3_5_7_9_11_13_15_17_19_. Здесь видна закономерность, что каждое последующее число больше предыдущего на 2.
Также существуют такие порядки: _3_7_15_31_63_127_ … или _5_11_17_26_29_35
И, конечно же: _2_6_14_30_62_126_и т.д.

Рис 53

Здесь возникает целый ряд числовых пропорций. Если взять за основу горизонтальные порядки, то параллельно можно увидеть и вертикальные порядки, где в каждом ряду последующая цифра больше предыдущей соответственно на 1, 2, 3, 4, 5, 6 и т.д.

Золотое число и обратное ему отличаются на единицу. Так что основных золотых чисел, строго говоря, – два: Ф и 1/Ф: умножая на Ф, или деля на 1/Ф, получишь один и тот же результат.

Но математика наука точная, поэтому при точных вычислениях получается:
Такое число: 1,6180339887498948482045868…

У золотой пропорции две формулы и два числа – мажорное (Ф) и обратное первому – минорное (Ф1):
Ф = (√5 + 1) : 2 = 1,618…
Ф1 = 1 : Ф = (√5 – 1) : 2 = 0,618…
И если Ф – решение квадратного уравнение x2 – x – 1 = 0,
то Ф1 – решение уравнения x2 + x – 1 = 0.

Умножая на число мажорного золота (Ф), или деля на минорное золото (1 : Ф), мы получим одинаковый результат. Следовательно, Ф1 – число, обратное Ф. и При этом не существует других чисел, которые были бы больше своего обратного ровно на единицу. И как мажорное золото на единицу больше минорного, квадрат мажорного золота на единицу больше его самого:
Ф2 = (√5 + 3) : 2 = 2,618…
Прогрессия вида 1, Ф, Ф2… Фn – не только геометрическая, это еще и арифметический ряд, в котором каждый его член, начиная с третьего, равен сумме двух предыдущих:
Ф2 = 1 + Ф
Ф3 = Ф2 + Ф
Ф4 = Ф3 + Ф2
Ф5 = Ф4 + Ф3

Итак, проследив в целом за порядками чисел можно увидеть 3 тенденции: первая функция состоит из чисел кратных 2 (четные числа), другая функция, где числа нечетные — такие как, 1,3,5,7 и третья состоит из смешанных чисел, как четных, так и нечетных, например: _3_6_9_12_15_18_.

Надо сказать, что древние культуры очень успешно использовали числовые пропорции в своей практической деятельности. К примеру, египтянам, приходилось каждый год (после разлива Нила) заново нарезать плодородные земли под наделы. Они применяли закон Евклида о построении треугольника с прямым углом. Треугольник со сторонами 3_4_5 имеет один прямой угол, и два острых. Этот же способ с узелками на веревке они применяли и при построении своей архитектуры.

В культуре майя и ацтеков длину мерили локтями или шагами. В древнем Риме народ измерял длину акрами, на Руси – аршинами и локтями, мореходы измеряли расстояния в милях.
Сейчас за эталон меры длины принят 1(один) метр.

Принципы формообразования в природе

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десяти сантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.

На примере раковины можно наблюдать пропорцию и схожесть в различных явлениях.

Рис 54 Раковина	Рис 55 Лестница -форма спирали

Рассматривая параметры тел во вселенной можно прийти к выводу, что восприятие этих объектов зависит как минимум от четырех факторов: длины, ширины и высоты (т.е. геометрических параметров) и нахождения тела в пространстве – т.е. времени. Три из этих факторов находятся в видимой части восприятия человека, четвертый параметр – время находится в сфере его эмпирического восприятия. Наблюдая приближающийся поезд, вначале мы видим геометрическую точку, потом тело, и наконец, проносящуюся массу, исчезающую в пространстве. Здесь, явно на лицо преобладание временного фактора, который в нашем сознании воспринимается как движущийся объект.

Развитие всех форм на планете Земля, находится под вселенским законом, открытым Фибоначчи, все развивается по спирали, и находится во взаимоотношении 1,618… или 0,618.

Числа золотого сечения, а это напомним 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и т.д., являются знаковыми не только для всего живого на земле, но и являются краеугольными в историческом аспекте.

И при этом, все в этом мире является относительным. Как говорил Герадот: «…нельзя дважды войти в одну и ту же воду».

—

Все в мире вибрирует и находится на своей частоте. Самой низкой частотой вибрации является твердое тело. По мере того, как частота возрастает, тело становится жидким, и газообразным. Следующий диапазон – звуковые и электромагнитные волны и тепловые волны. Следом идут световые волны. Человек видит только малую часть спектра –это 360-780n. Эта видимая часть спектра и является цветовой радугой, которую воспринимает человеческий глаз.

Затем цветовой спектр становится невидимым человеческому глазу – он называется ультрафиолетовые лучи, рентгеновские лучи, и потом гамма-излучение. И самыми последними являются реликтовое или космическое излучение.

Рис 56

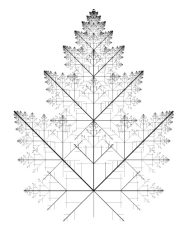
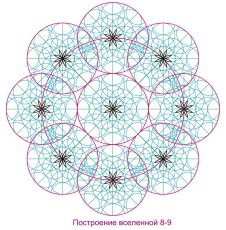
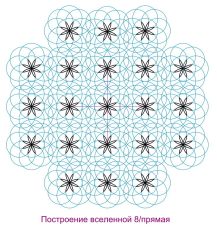
Построения космических узоров разрастания вселенной

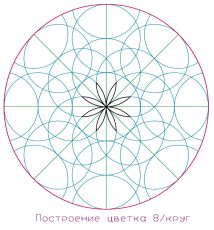
Рис 57	Рис 58	Рис 59

Разрастание и построение происходит от малых частиц к образованию средних скоплений и образование больших форм и скоплений. Все состоит из нано и микро формообразующих частиц — до приумножения и разрастания до бесконечности.

«Что было, то и будет, и что творилось, то творится,
И нет ничего нового под солнцем.» Экклисиаст, глава 9

Рис 60	Рис 61	Рис 62

Как менялись пропорции в построении человеческого женского образа.

Рис  63-Голова Ботхисатвы	Рис 64-Голова Афины Древняя Греция	Рис 65-Голова Амазонки (Поликлет) Греция

Как мы видим, какова бы ни была эпоха, и чувство пропорции и гармонии, присущие тому времени и народу, везде ярко проявляет себя красота, даря миру шедевры вечных образов.

Ждите продолжения, где мы коснемся, таких тем, как керамика, живопись, одежда, фотография, и другое.

*Все материалы взяты из открытых источников.

Литература:

1. «Имена: определение характера и судьбы» / Веря Склярова /-М:АСТ:Астрель, 2011.Вера Склярова –одна из самых опытных тарологов – магов.

2. «Нумерология: выигрышные числа и нумерологическая совместимость/Лия Робин/ М:РИПОЛ классик, 2008.
3. Практическая энциклопедия фэн-шуй» /перевод с английского –А.Блейз / ОЛМА-ПРЕСС / ,2001.
4. Статьи в интернете г-на Чернова вот ссылки http://chernov-trezin.narod.ru/ вот ссылка на его статьи.
5. Выдержки из книги Сергея Леонидовича Панфилова посвященные семиуголнику.
6. Выдержки из статьи Виктора Лавруса «Золотое Сечение».
7. Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989.
8. Кеплер И. О шестиугольных снежинках. – М., 1982.
9. Дюрер А. Дневники, письма, трактаты – Л., М., 1957.
10. Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.
11. Стахов А. Коды золотой пропорции.
12. Статьи и выдержки взятые из свободного доступа в интернете: «Векипедия», статьи по античной литературе.